法則性を発見するたのしみ
平成14年2月に細水保宏先生が筑波大学附属小学校6年生を対象に行った「数と図形の不思議」という授業の,中学校での追試バージョンです。算数・数学の得意・不得意に関係なく,みんなでワイワイ盛り上がる最高の教材です。
大学でも文型の学生相手に追試しましたが,やはり大盛り上がりでした。
②③④の立方体と頂点や辺,面の関係などの法則性に気づくことができれば言うことなしというわけです。
できれば,「サイコロキャラメル」と絵具代わりのピンクの付箋紙,A4のメモ用紙を準備して,授業を始めましょう。
法則性を発見するたのしみ
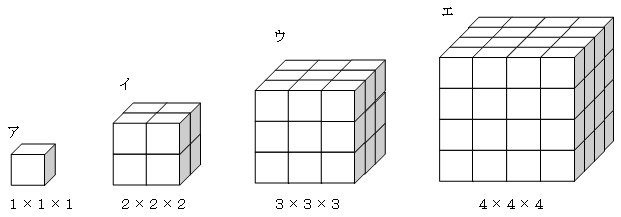
問1 1辺が1cmの立方体の積み木を組み合わせて作った大きな立方体の表面に赤い色を塗ります。
そのあと,元の小さな積み木にもどします。
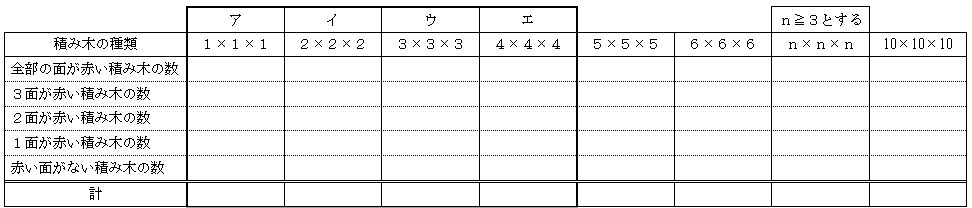
次の積み木の数を数え,下の表を完成しよう。
① 全部の面に赤い色が塗られたもの
② 3面に赤い色が塗られたもの
③ 2面に赤い色が塗られたもの
④ 1面に赤い色が塗られたもの
⑤ 赤い色が塗られていないもの
問2 答えが合っているかどうか確かめる方法も考えよう。それぞれの積み木の数の求め方にきまりがあれば,それも見つけよう。
問3 10×10×10の大きな立方体について,①から⑤の数を数えましょう。
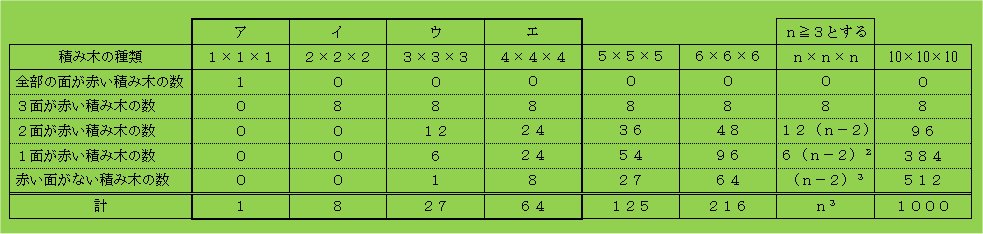
■ 正解は次のとおり
n角形の欄の12(n-2)や6(n-2)2,(n-2)3,n3の式の意味するところを, 子どもたちなりに自分の言葉で説明できるようになれば,最高ですね!