約数の数は何個?
約数の数は何個? 力勝負か,頭脳勝負か?
たとえば,42の約数の数を求める場合,次の3つの方法で解くことが予想されます。
A君の場合 ⇒ 小さい順番に約数を書き出していく。 ⇒ 1,2,3,4,6,7,14,……B君の場合 ⇒ 1の次に42,2の次に21のように両端から約数を書き出していく。
⇒ 1,2,…,…, ,…,…,21,42
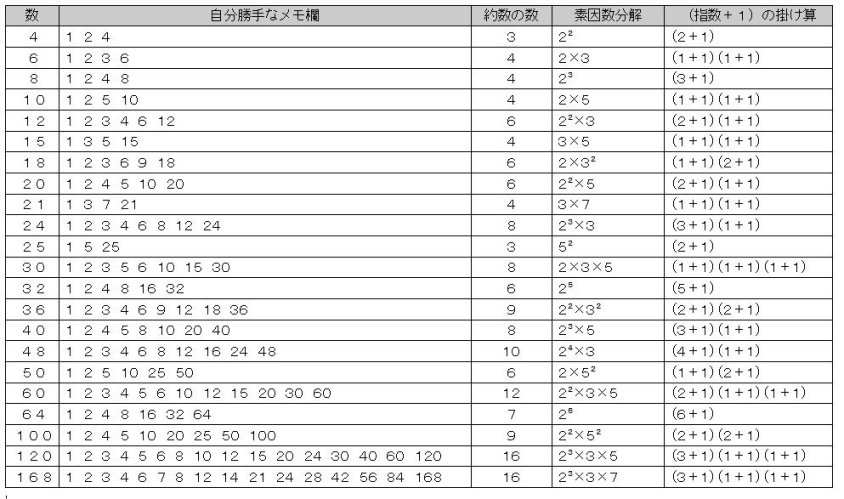
C君の場合 ⇒ 2×3×7と素因数分解し,それぞれの ≪指数+1≫ を乗じて,2×2×2=8とし,約数の数を8個と求める。
A君の方法で解いている生徒には,B君の方法のよさ(数えもれがない)に気付かせたい。
B君の方法をマスターした上で,C君の方法で検算を行うことができれば最高。C君の方法だけで済ませないように助言したい。
数学が苦手な生徒に対しては,B君の方法をきちんとマスターできれば十分であることを伝え,自信を持たせたい。
正解は次のとおり
※ 右端の『(指数+1)の掛け算』の結果が,『約数の数』と等しくなっています。C君のこの方法とB君の方法を併用するといいですね。