濃度問題もこれで楽勝-サトウのシーソー理論
中学校の数学でつまずく単元と言えば,泣く子も黙る「連立方程式の濃度問題」でしょう。しかし,子どもの頃によく遊んだシーソーを思いだせば,いとも簡単に解くことができます。
1 具体的な生活体験を,数学に生かそう
このサイト名(tanbowaii)にあるように,周りが田んぼだらけの農家に育った私は,小学校時代から,暗くなるまで田畑で働くのが 日常でした。夏の盛りは,トマトやきゅうり,ナスなどの消毒や収穫に忙しい季節でしたが,父親に言いつけられて消毒薬の原液と水を混ぜて消毒液を作り, 噴霧器を肩に担いで,右腕の感覚がなくなるまで消毒をしたものでした。
そのときの体験から「水を多くすればするほど薄い消毒液になり,水を少なくすれば濃い消毒液になる」ことは,自明の真理でした。
まして,食塩水の濃度はつりあいで決まることは,当然のことだったわけです。
その農業体験から考え出したのが 「サトウのシーソー理論」 でした。
2 実際に授業で指導してみて
私自身が中学時代に自分で考え出して使っていた解き方ですが,数学の補欠に学級に入ってこの解き方を紹介すると,あまりの簡単さに, 「ホントにこれで大丈夫なの?」と,英語教師の私を疑っている様子です。それでは,具体的な問題でやってみましょう。
問1 12%の食塩水300グラムと24%の食塩水150グラムを混ぜると,何%の食塩水ができますか。
次の手順で,シーソーの図を描いてください。
1 食塩水の濃度12%と24%を,シーソーの両端にとります。2 食塩水の重さをそれぞれの濃度の下に付けます。
3 重さをできるだけ簡単な比で表すのがコツです。
※ ここでは,300:150=2:1となり,おもり2個と1個になります。
4 上の比の合計3(2+1=3)でシーソーを3等分します。→16%,20%のところで3等分します。
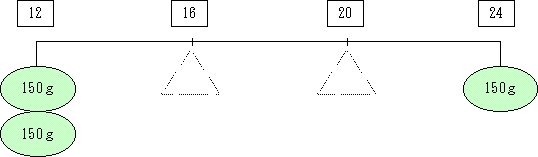
5 シーソーの両端の重さを考え,つりあいの点に三角(ピンク色)を書き込みます。
6 その三角の上の%が,できる食塩水の濃度になります。
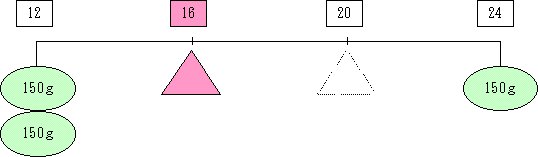
今度は,できた食塩水の濃度をa%として,方程式を立て,実際に解いてください。
答はシーソー理論で分かっていますから,自信を持って解けるはずです。簡単ですね。300×12/100+150×24/100=(300+150)×a/100
両辺に100をかけて,分母を払います。
300×12+150×24=(300+150)×a
3600+3600=450a
450a=7200
a=16
ほら,やっぱり16%になりました。簡単ですね。
それでは,もう一問,やってみてください。
問2 12%の食塩水375グラムと24%の食塩水125グラムを混ぜると,何%の食塩水ができますか。
A: 答はこちらです。クリックして確認してください。3 未知数が二つの本格的な連立方程式の場合
問3 12%の食塩水aグラムと24%の食塩水bグラムを混ぜたら,21%の食塩水が80グラムできました。それぞれ何グラム混ぜましたか。
次の手順で,シーソーの図を描いてください。
1 食塩水の濃度12%と24%を,シーソーの両端にとります。
2 つりあいの位置21%のところに三角を描きます。
3 支点をはさんだシーソーを長さを,できるだけ簡単な比で等分します。
※ ここでは,12%,21%,24%なので,3:1となり,シーソーを4等分します。
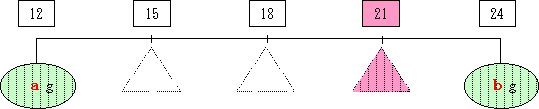
4 できた食塩水80グラムを4等分(シーソーの目盛分)し,おもり一つ当たりの重さを確認します。
※ ここでは,80グラム÷4=20グラム。Cは20グラム。
5 12%の食塩水は20グラム,24%の食塩水は60グラムであることが分かります。
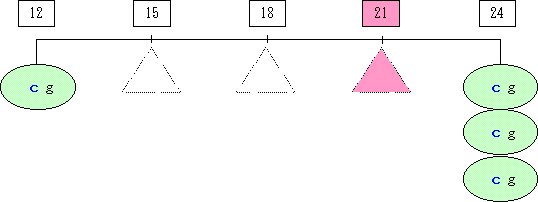
12%の食塩水の量をaグラム,24%の食塩水の量をbグラムとして,方程式を立てて,解いてください。
a×12/100+b×24/100=80×21/100 a+b=80
両辺に100をかけて,分母を払います。
a×12+b×24=80×21 b=80-a
a×12+(80-a)×24=80×21
12a+1920-24a=1680
-12a=-240
a=20,b=80-20=60
ほら,やっぱり12%の食塩水は20グラム,24%の食塩水は60グラムとなりました。簡単ですね。
それでは,練習問題です。